

문제 분석
3가지의 경우의수에 따라서 큐에 다시 담아줘서 최소값을 구했다.
전체 소스
package test;
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int input = Integer.parseInt(br.readLine());
int count = 0;
Queue<int[]> q = new LinkedList<>();
q.offer(new int[] {input,0});
int min = Integer.MAX_VALUE;
while(!q.isEmpty()) {
int[] position = q.poll();
input = position[0];
count = position[1];
// System.out.println(input+" "+count);
if(input == 1) {
if(min>count) {
min = count;
}
continue;
}else if(count>=min) {
continue;
}
if(input%2==0) {
q.offer(new int[] {input/2,count+1});
}
if(input%3==0) {
q.offer(new int[] {input/3,count+1});
}
if(input>1 ) {
q.offer(new int[] {input-1,count+1});
}
}
System.out.println(min);
}
}
문제 분석2
위와 같은 경우 모든 경우의수를 다 탐색하는 완전탐색의 방법이라고 할 수 있다.
문제를 풀고 난뒤 알고리즘 분류를 보니 다이나믹 알고리즘인것을 보고 해당 방법을 찾았다.
각 수에 대한 최소값을 나열해보자
1 2 3 4 5 6 7 8 9 10
0 1 1 2 3 2 3 3 2 3
2와 3으로 나눠떨어질경우 그 나눠떨어진거에서 +1만 해주면 그 수를 완성 시킬 수 있다.
즉 9의경우 3으로 나누면 3이되는데 3을 가기까지 1번의 연산이 사용되니까 +1 한 2번이 값이된다.
일단 기본적으로 해당 횟수를 구해야하는데 -1 할 때마다 1번의 연산을 사용하니 그 전의 수보다 1번의 기회를 기본적으로 사용한다.
즉 3으로 나눌수 있는 규칙이 없다면 9의 경우 8보다 +1 연산을 더해서 4번의 연산이 필요할 것이다.
위와 같은 규칙으로 푼 방법이다.
전체 소스2
package test;
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int input = Integer.parseInt(br.readLine());
int[] p = new int[input + 1];
p[1] = 0;
for(int i = 2; i <= input; i++) {
p[i] = p[i - 1] + 1;
if(i % 2 == 0 && p[i] > p[i / 2] + 1) {
p[i] = p[i / 2] + 1;
}
if(i % 3 == 0 && p[i] > p[i / 3] + 1) {
p[i] = p[i / 3] + 1;
}
}
System.out.println(p[input]);
}
}
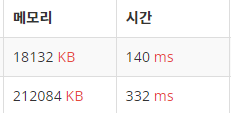
1번 방법과 2번방법의 메모리와 시간 비교이다. 완탐을 하지 않으니 메모리와 시간사용이 확연하게 줄은것을 확인 할 수 있다.
문제
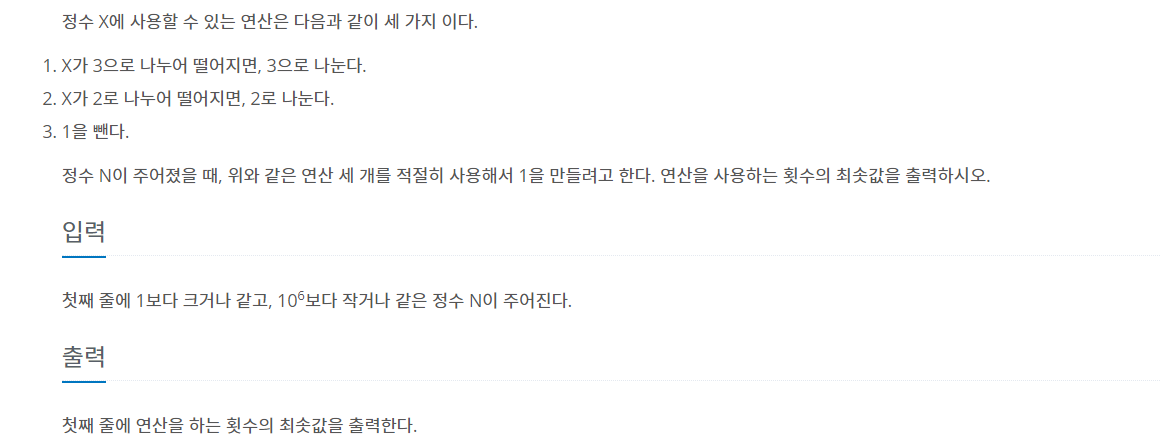
예제 입력 1
2
예제 출력 1
1
예제 입력 2
10
예제 출력 2
3'알고리즘(BOJ) > Silver' 카테고리의 다른 글
| 백준 1, 2, 3 더하기 9095 다이나믹 (0) | 2023.03.23 |
|---|---|
| 백준 - 이친수 2193 (다이나믹) (0) | 2023.03.18 |
| 백준 - 물병 1052 (0) | 2023.03.14 |
| 백준 - 스네이크버드 16435 (0) | 2023.03.10 |
| 백준 - A -> B 16953 (0) | 2023.03.09 |